Colpitts Oscillator Derivation

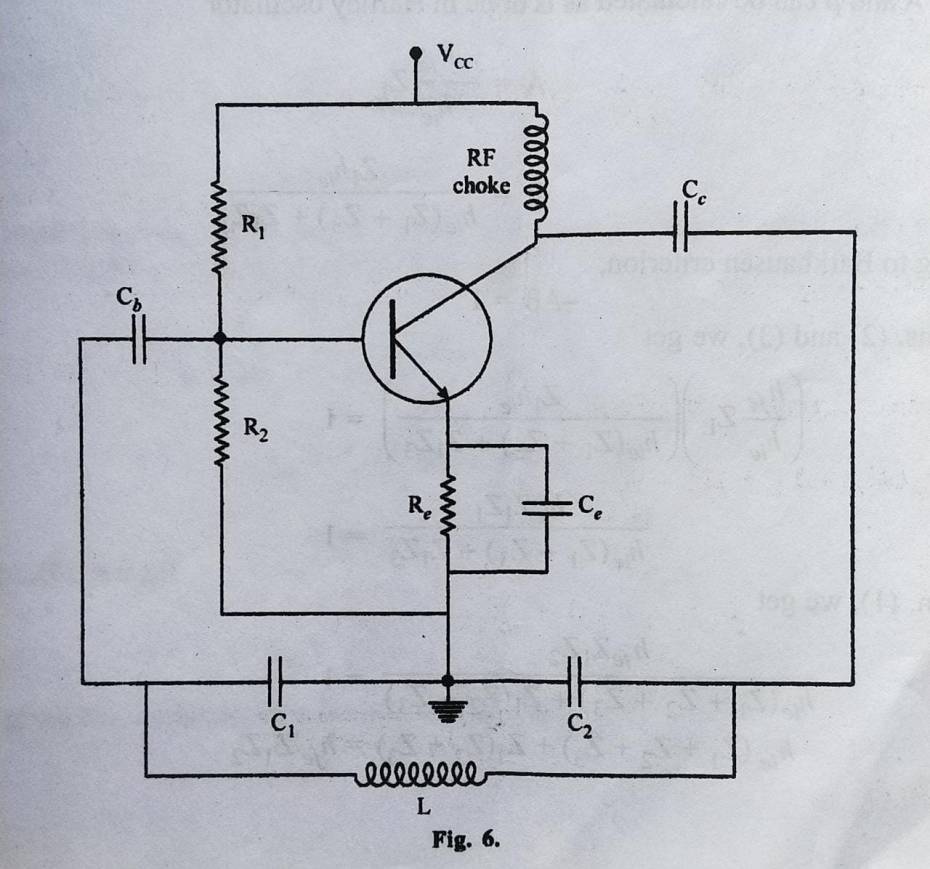
Fig. 6 Shows the circuit diagram of Colpitts oscillator.

What is Colpitts Oscillator?

In this oscillator, tank circuit consists of C₁,C₂, and L. Stabilized self-bias to the amplifier is provided by R₁ R₂ R_e and C_e. Radio frequency (RF) choke is used to permit an easy flow of d.c., whereas a capacitor C_c permits a.c. to flow from the collector to the tank circuit.

The transistor in common emitter configuration introduces a phase shift of 180^o between the input and output voltages. Another phase shift of 180^o is provided by the capacitive feedback. Hence the net phase shift of 360^o or 0^o is introduced between the input and output voltages, leading to positive feedback.

Working of Colpitts Oscillator

When the circuit is connected to the supply V_CC , capacitors C₁ and C₂ are charged. After fully charged, these capacitors discharge through the inductor of inductance L. Hence damped oscillations are produced. The voltage across C₁ is applied to the base emitter circuit which appears in the amplified form in the collector circuit. This voltage compensates the energy loss continuously in the tank circuit and hence undamped oscillations of definite frequency are obtained at the output. 

Colpitts Oscillator Derivation

The equivalent circuit of Colpitss oscillator is shown in fig. 7.

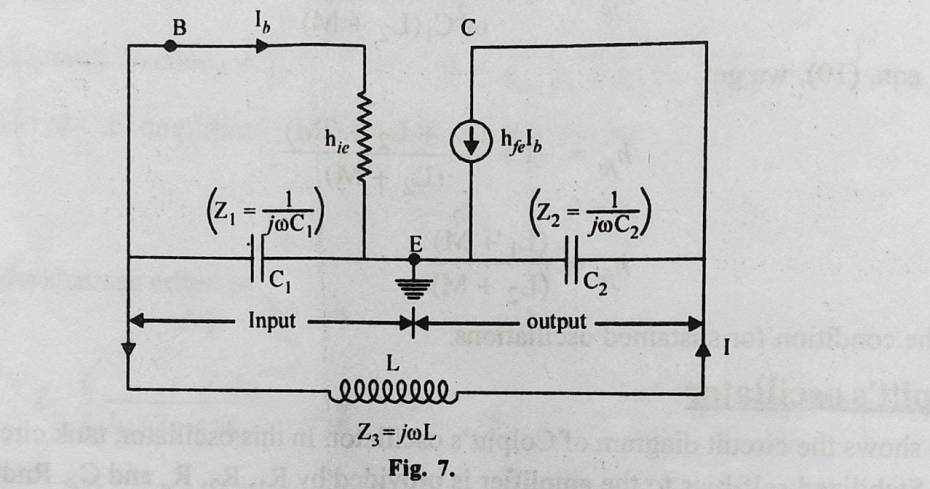
Load impedance between output terminal can be calculated in the same manner as is done in Hartley oscillator.

Similarly, A and β can be calculated as is done in Hartley oscillator.

According to Barkhausen criterion,

-Aβ = 1

using eqns. (2) and (3), we get

Using eqn. (1), we get

Eqn. (4) becomes

Comparing the imaginary parts of eqn. (5), we get

Since ω = 2πf

Which is the expression for the frequency of oscillations produced in the Colpitts oscillator.

Now comparing the real parts of eqn. (5), we get

using eqn. (6) we get

Eqn. (8) gives the condition for sustained oscillations.